Modelo de Três Fatores

O modelo de três fatores de Fama e French, surgido principalmente a partir de um artigo dos autores no Journal of Finance em 1992 (The Cross-Section of Expected Stock Returns), é utilizado para explicar os retornos de ações e é uma alternativa ao CAPM. Ao invés de utilizar um fator (o retorno em excesso do mercado, retorno das ações menos a taxa livre de risco) utiliza mais dois fatores de risco.

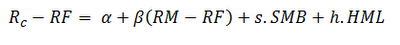
O principal ponto do primeiro artigo é a consolidação do que os autores e outros acadêmicos já vinham pesquisando, a análise da capacidade do modelo de fator único de explicar satisfatoriamente os retornos das ações e o poder preditivo de outras variáveis como o tamanho. Fama e French propõem um conjunto de variáveis tais como a relação entre o valor contábil e o valor de mercado (VPA/P) das ações, o valor de mercado, o índice Lucro/Preço (L/P) e a alavancagem da empresa que poderiam melhor explicar a diferença de retornos.

O primeiro teste mostrado no artigo foi montar dez carteiras de acordo com o tamanho das empresas (medido pelo valor de mercado). Esse teste mostra uma relação negativa entre tamanho e retornos e positiva entre retornos e o beta de mercado do CAPM. Antes de oferecer validade para a relação entre beta e retorno, esse teste mostra que as variáveis beta e tamanho são altamente correlacionadas. No artigo, a tabela de referência é a II.

Na mesma tabela II, separando as ações com base nos betas, não há mais a relação positiva entre retornos e beta. A tabela I mostra outro conjunto de testes para tentar separar o efeito do tamanho nos retornos do efeito do beta. Para isso, foram montadas 100 carteiras dividindo as ações em 10 categorias de betas e 10 de tamanho. O retorno diminui conforme o tamanho da empresa aumenta, mas não há uma relação positiva consistente entre beta e retorno. Na verdade, nos extremos (menor beta x maior beta) para cada categoria de tamanhos o retorno das ações com menor beta é maior do que o retorno das ações de maior beta.

Em regressões múltiplas que procuram explicar os retornos das ações, em nenhuma das duas análises que contam com o beta de mercado (apenas o beta e o beta mais o logaritmo do tamanho) o coeficiente é estatisticamente significativo e em um é negativo ao invés de positivo.

As análises com a relação VPA/P resultam em coeficientes positivos e significativos, confirmando que ações com maiores valores para esse indicador (e menores relações Preço/Valor Patrimonial) obtêm maiores retornos. Essa relação se estabelece também com carteiras montadas baseadas no indicador, aquelas com maiores VPA/P obtendo maiores retornos (sem grandes diferenças no beta). O mesmo ocorre com a relação L/P (o inverso do P/L) na análise de regressão, mas não separando as carteiras em termos de L/P. Na análise multivariada, quando se inclui VPA/P e L/P, apenas o VPA/P é estatisticamente significativo. Por conta disso, a variável que melhor explica os retornos é VPA/P. A tabela da regressão é a III e a comparação do VPA/P e do L/P é feita na tabela IV.

A última variável analisada no artigo é a alavancagem. Foram utilizadas alavancagens com valores contábeis e de mercado. Na análise multivariada, a alavancagem de mercado tem coeficiente positivo e a contábil negativo, ambos estatisticamente significativos. Subtraindo um do outro, por definição, passa a ser o VPA/P (na verdade, da forma como foi feita, o logaritmo do indicador). Ou seja, analisar a alavancagem é analisar o VPA/P.

Logo, sobraram duas variáveis que explicam bem os retornos: tamanho e VPA/P. A construção de carteiras com base nessas duas variáveis mostra que, para um determinado tamanho, maior VPA/P aumenta os retornos e, para um determinado VPA/P, menor tamanho aumenta o retorno. A exceção fica por conta do baixo VPA/P, com as ações maiores rendendo mais. A tabela de referência é a V.

Por fim, a regressão com esses dois fatores sempre gera coeficientes com os sinais esperados (negativo para tamanho, positivo para VPA/P) e estatisticamente significativos, o mesmo não ocorrendo para o beta na análise com os três fatores (sinal negativo e não significativo).

Esse artigo daria origem a outro artigo publicado em 1993 pelos mesmos autores (Common risk factors in the returns on stocks and bonds). Dessa vez, o objetivo é criar um modelo alternativo ao CAPM que melhor explique a variação do retorno de ativos (ações e títulos de renda fixa).

Os autores separam as ações em três grupos com diferentes VPA/P (30% menores, 30% maiores, 40% entre os dois), excluindo ações com patrimônio líquido negativo, e dois grupos com diferentes tamanhos (50% menores e 50% maiores). Com isso, criam a carteira SMB (small minus big), formada como a diferença entre o retorno das 50% menores ações e o retorno das 50% maiores, e a carteira HML (high minus low), formada como a diferença entre o retorno das ações com alto VPA/P e o retorno das ações com baixo VPA/P (excluindo dessa carteira as ações com VPA/P médio). Além disso, há o prêmio por risco do CAPM, com o retorno do mercado definido como o retorno das ações nos seis grupos do cruzamento entre tamanho e VPA/P mais as ações com patrimônio líquido negativo (ou seja, todas as ações da base) e o retorno sem risco sendo a taxa do Treasury Bill de um mês. Há ainda variáveis relativas à renda fixa e testes para explicar o retorno de títulos de renda fixa, que serão pouco explorados aqui. Os testes são feitos para explicar os retornos de 25 carteiras formadas pelo cruzamento de cinco categorias de tamanho e cinco categorias de VPA/P. A metodologia é a regressão linear tendo como variável dependente o retorno da carteira em análise (as 25 carteiras analisadas individualmente) menos a taxa sem risco e como variáveis independentes os fatores de risco (prêmio por risco, SMB, HML e variáveis de renda fixa).

A tabela 1 do artigo apenas mostra algumas estatísticas sobre as 25 carteiras que serão analisadas. A tabela 2 mostra os prêmios por risco médios (RM-RF, SMB, HML) e os retornos em excesso das 25 carteiras, com os retornos diminuindo com o tamanho e aumentando com o VPA/P. Os resultados mais importantes começam na tabela 3 e vão até a tabela 8b, testando diversas especificações de modelos de regressão. A tabela 3 mostra a regressão utilizando os fatores de risco associados à renda fixa, que possuem significância estatística, mas explicam pouco da variação dos retornos (baixo r-quadrado). Na tabela 4, o fator de risco analisado é o prêmio por risco à lá CAPM, com o beta sendo estatisticamente significativo, mas os r-quadrados ainda baixo (entre 61% e 92% com apenas dois iguais ou superiores a 90%). A tabela 5 mostra os resultados das regressões apenas com SMB e HML, com resultados piores do que o CAPM (r-quadrado entre 0,04% e 0,65%). Porém, juntando os três fatores (prêmio por risco, SMB e HML) conforme a tabela 6, os r-quadrados melhoram significativamente, ficando entre 83% e 97%. O comportamento dos coeficientes está coerente com os resultados obtidos no artigo de 1992, sem haver uma relação muito clara entre betas e retornos, mas havendo relação negativa entre tamanho e retornos e (principalmente) relação positiva entre VPA/P e retornos. Na verdade, a tabela 6 apenas mostra o valor dos coeficientes, tendo que haver um cruzamento imaginário entre a tabela 6 e a parte da tabela 2 que mostra os retornos em excesso.

Os resultados da tabela 6 são os melhores encontrados no artigo e geram o modelo de três fatores Fama-French definido como:

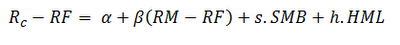
Onde:
s = Coeficiente de regressão relacionado com o SMB

h = Coeficiente de regressão relacionado com o HML

As tabelas 7 e 8 voltam a incluir os fatores relativos à renda fixa. Esses fatores até são estatisticamente significativos, mas não melhoram os r-quadrados do modelo de três fatores, de forma que, para explicar o retorno das ações, três fatores bastam.

A tabela 9 mostra o intercepto das regressões (o alfa), análogo ao alfa de Jensen do CAPM. Para o modelo de três fatores, apenas três alfas são estatisticamente diferentes de zero ao nível de 10%. Com isso, o intercepto não tem papel relevante nos modelos e os três fatores explicam a variação do retorno das ações. A tabela 9c mostra que os alfas utilizando o modelo de três fatores para ações e renda fixa é diferente de zero ao nível de 5%. Nas palavras dos autores, “isso mostra que o modelo de três fatores é apenas um modelo, isso é, é falso”. Falseável como todo modelo, esses três fatores são úteis para explicar o retorno de ações, embora algumas classes de ações não tenham sido bem explicadas nessa análise (particularmente, as ações pequenas e de baixo VPA/P com desempenho negativo e ações grandes e de baixo VPA/P com bom desempenho).

O restante do artigo discute outros efeitos que poderiam afetar os resultados. Na seção 6.1. é refutada a hipótese de que outras variáveis (como a relação Dividendo/Preço) melhorem o modelo de três fatores, a seção 6.2. mostra que os três fatores explicam o efeito Janeiro, a 6.3. muda um pouco a divisão em 25 carteiras sem alterar os resultados, a seção 6.4. classifica as ações em termos de L/P e a seção 6.5. em termos de Dividendo/Preço, os três fatores ainda explicando satisfatoriamente a variação dos retornos.

Esse modelo pode ser utilizado como uma alternativa ao CAPM, principalmente na análise dos retornos de carteiras ou ativos, analisando se o alfa da carteira ou do ativo é significativamente diferente de zero, indicando habilidade ou incompetência do gestor ou ineficiência de mercado. O modelo é muito utilizado para medir o retorno anormal de carteiras, inclusive em artigos já comentados aqui. Pode ser utilizado também para seleção de carteiras, mensurar retornos anormais em estudos de evento e estimar o custo de capital das empresas (pouco usado).

Tweet