Marcas e Empresas
wi = Peso do ativo i na carteira
σi,j = Covariância entre o ativo i e o ativo j.
A covariância é definida por:
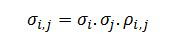
Onde:
ri = Retorno do ativo i
Sujeito a:
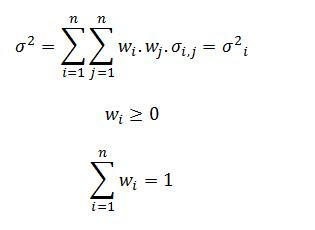
- Com Quantas Ações Se Faz Uma Carteira Bem Diversificada?
Desde o trabalho seminal de Harry Markowitz que o potencial de redução de risco proporcionado pela diversificação está bem estabelecido. Uma questão mais prática é: precisamos de quantas ações para obter uma carteira “bem diversificada”....
- Estilos De Investimentos
Em artigopublicado no Journal of Portfolio Management em 1978, William Sharpe explica sobre os estilos de investimentos de uma maneira interessante e bastante técnica. Basicamente, são quatro estilos de investimentos listados por Sharpe, gestão passiva...
- Avaliação De Desempenho De Carteiras
Os modelos do texto anterior podem ser modificados para se tornarem medidas de desempenho de carteiras. Podem ainda ser utilizados para analisar retornos de ativos individuais (carteiras de um ativo), sendo que isso não é comum para os dois primeiros....
- βeta
No cálculo de retornos exigidos de ações para avaliação de empresas (taxa de desconto), gestão de investimentos (retorno esperado) ou finanças corporativas (custo do capital próprio), usa-se comumente a seguinte fórmula: Retorno Exigido: Taxa...
- Risco E Retorno (renda Variável)
Risco e Retorno são dois conceitos essenciais em Finanças, conceitos intimamente ligados. Esse post tratará especificamente do risco e do retorno para ativos de renda variável, não tratando da renda fixa. O retorno passado de um ativo é a sua valorização...
Marcas e Empresas
Seleção de carteiras
(Portfolio Selection)
Harry Markowitz
Journal of Finance. Volume 1. 1952
O texto anterior tratou dos retornos em condições de certeza, onde o retorno é apenas a compensação pelo adiamento de consumo (valor do dinheiro no tempo). Agora, a discussão segue para a incorporação do risco na análise dos retornos dos ativos, onde os retornos passariam a ser também uma compensação pelo risco incorrido. O primeiro passo (este texto) é um resumo do artigo clássico de Markowitz, considerado a base da Teoria das Carteiras. O segundo (um futuro texto) seria a combinação de taxa livre de risco e ativos de risco, resultando na Capital Market Line de Lintner e a Security Market Line de Sharpe. Os comentários deste texto reproduzem os argumentos de Markowitz e também alguns comentários adicionais meus.
Segundo o autor, a escolha de carteiras de investimentos é feita em duas etapas: a primeira começa com observação e experiência e termina com alguma expectativa sobre os retornos futuros. A segunda etapa começa com as expectativas futuras e termina com a seleção de carteiras. O autor foca nesse artigo a segunda etapa.
O autor primeiro rejeita que o critério de seleção deva ser a maximização dos retornos esperados. Essa análise implica a alocação total em um único ativo, ignorando o risco e a possibilidade de reduzi-lo com a diversificação. Como o retorno futuro é desconhecido, trabalha-se com “retornos esperados”. Um retorno esperado é uma média e deve-se considerar a variabilidade dos retornos em torno dessa média nas decisões de investimento. Logo, um processo que ignore a variabilidade dos retornos em torno dos valores esperados não leva às melhores decisões.
Com base nisso, o autor sugere a regra do retorno esperado-variância (que futuramente seria chamado apenas de média-variância). O retorno de uma carteira é a média ponderada pela participação na carteira dos retornos dos ativos individuais que a compõem. O risco, porém, não é uma média ponderada já que a correlação dos retornos de um ativo com os retornos de outro acaba por compensar algumas variações em direções opostas dos ativos. Isso é mais discutido ao final do texto.
A variância de uma carteira composta por n ativos é dada por:
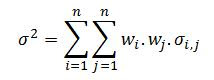
Onde:Harry Markowitz
Journal of Finance. Volume 1. 1952
O texto anterior tratou dos retornos em condições de certeza, onde o retorno é apenas a compensação pelo adiamento de consumo (valor do dinheiro no tempo). Agora, a discussão segue para a incorporação do risco na análise dos retornos dos ativos, onde os retornos passariam a ser também uma compensação pelo risco incorrido. O primeiro passo (este texto) é um resumo do artigo clássico de Markowitz, considerado a base da Teoria das Carteiras. O segundo (um futuro texto) seria a combinação de taxa livre de risco e ativos de risco, resultando na Capital Market Line de Lintner e a Security Market Line de Sharpe. Os comentários deste texto reproduzem os argumentos de Markowitz e também alguns comentários adicionais meus.
Segundo o autor, a escolha de carteiras de investimentos é feita em duas etapas: a primeira começa com observação e experiência e termina com alguma expectativa sobre os retornos futuros. A segunda etapa começa com as expectativas futuras e termina com a seleção de carteiras. O autor foca nesse artigo a segunda etapa.
O autor primeiro rejeita que o critério de seleção deva ser a maximização dos retornos esperados. Essa análise implica a alocação total em um único ativo, ignorando o risco e a possibilidade de reduzi-lo com a diversificação. Como o retorno futuro é desconhecido, trabalha-se com “retornos esperados”. Um retorno esperado é uma média e deve-se considerar a variabilidade dos retornos em torno dessa média nas decisões de investimento. Logo, um processo que ignore a variabilidade dos retornos em torno dos valores esperados não leva às melhores decisões.
Com base nisso, o autor sugere a regra do retorno esperado-variância (que futuramente seria chamado apenas de média-variância). O retorno de uma carteira é a média ponderada pela participação na carteira dos retornos dos ativos individuais que a compõem. O risco, porém, não é uma média ponderada já que a correlação dos retornos de um ativo com os retornos de outro acaba por compensar algumas variações em direções opostas dos ativos. Isso é mais discutido ao final do texto.
A variância de uma carteira composta por n ativos é dada por:
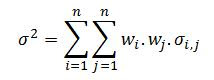
wi = Peso do ativo i na carteira
σi,j = Covariância entre o ativo i e o ativo j.
A covariância é definida por:
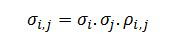
Onde:
ρi,j = Correlação entre o ativo i e o ativo j
σi = Desvio Padrão dos retornos do ativo i
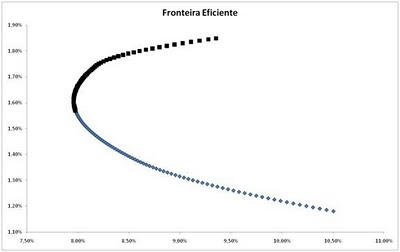
Uma forma de representar as possíveis combinações de risco e retorno de carteiras é através de um gráfico Risco x Retorno.
ρi,j = Correlação entre o ativo i e o ativo j
σi = Desvio Padrão dos retornos do ativo i
Uma forma de representar as possíveis combinações de risco e retorno de carteiras é através de um gráfico Risco x Retorno.

A curva começa com uma carteira 100% investida no ativo de menor retorno. Vai-se diminuindo a proporção desse ativo na carteira com a inclusão (ou aumento da proporção) de ativos mais arriscados e, por conta do efeito da diversificação, o risco diminui e o retorno aumenta. Chega um determinado ponto onde o aumento na proporção dos outros ativos aumenta o retorno, mas também o risco. Esse é o começo da Fronteira Eficiente, que mostra as combinações de ativos que maximiza o retorno dado um risco. No gráfico acima, a fronteira eficiente está marcada com pontos escuros e as carteiras ineficientes com pontos azuis. Não seria possível obter uma combinação acima dessa fronteira eficiente, mas é possível obter uma combinação abaixo dessa linha, indicando carteiras ineficientes que poderiam ter seu retorno aumentado sem aumento no risco ou uma redução no risco sem redução no retorno.
A construção desse gráfico é feita em termos de risco e retorno esperados. Dessa forma, não há carteira que possa se situar acima da fronteira eficiente em termos esperados, embora isso possa ocorrer efetivamente. Utilizando-se os dados efetivos futuros, pode ser que uma carteira tenha um resultado tal que se situaria acima da fronteira eficiente construída em termos esperados, bastando que a carteira seja composta por ativos que tenham retornos superiores aos esperados e riscos não muito superiores (ou até inferiores) aos esperados.
A construção da fronteira eficiente pode ser feita no próprio Excel através do suplemento Solver (ou com macro em VBA que incorpore o Solver). Existem programas que realizam o cálculo automaticamente. Para cada ponto da curva, o problema passa a ser:
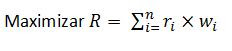
A construção desse gráfico é feita em termos de risco e retorno esperados. Dessa forma, não há carteira que possa se situar acima da fronteira eficiente em termos esperados, embora isso possa ocorrer efetivamente. Utilizando-se os dados efetivos futuros, pode ser que uma carteira tenha um resultado tal que se situaria acima da fronteira eficiente construída em termos esperados, bastando que a carteira seja composta por ativos que tenham retornos superiores aos esperados e riscos não muito superiores (ou até inferiores) aos esperados.
A construção da fronteira eficiente pode ser feita no próprio Excel através do suplemento Solver (ou com macro em VBA que incorpore o Solver). Existem programas que realizam o cálculo automaticamente. Para cada ponto da curva, o problema passa a ser:
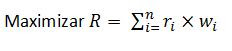
Onde:
ri = Retorno do ativo i
Sujeito a:
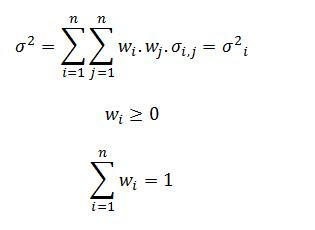
Ou seja: o que se busca é maximizar o retorno dado um nível de risco. A restrição de peso positivo indica que não é possível a venda a descoberto (que resultaria em peso negativo) e a restrição da soma dos pesos ser 1 indica não ser possível nem alocar capital fora das opções disponíveis nem tomar emprestado para aumentar as aplicações. Essas restrições podem ser modificadas, mas Markowitz não o fez nesse artigo.
A principal implicação desse artigo é o poder da diversificação. Porém, a diversificação deve ser do “tipo certo”, nas palavras do autor. Não é muito útil diversificar com diversas ferrovias ou diversas mineradoras na mesma carteira, já que a correlação entre as ações do mesmo setor é alta, de forma que todas vão mal ou bem ao mesmo tempo. Caso a correlação seja baixa, quando uma ação sobe a outra cai ou sobe menos e quando uma cai a outra sobe ou cai menos, de forma a diminuir a variação absoluta do retorno da carteira.
Com base em uma expectativa de retorno formada de alguma maneira (não analisada neste artigo), deve-se escolher os ativos para compor a carteira e seus respectivos pesos, levando em conta a variabilidade esperada dos retornos (o desvio-padrão dos retornos). Essa variabilidade dos retornos em torno da média é uma medida do risco de uma ação e o risco de uma carteira pode ser reduzido através da diversificação. O que se deseja na composição de uma carteira é maximizar o retorno esperado dado um nível de risco.
A principal implicação desse artigo é o poder da diversificação. Porém, a diversificação deve ser do “tipo certo”, nas palavras do autor. Não é muito útil diversificar com diversas ferrovias ou diversas mineradoras na mesma carteira, já que a correlação entre as ações do mesmo setor é alta, de forma que todas vão mal ou bem ao mesmo tempo. Caso a correlação seja baixa, quando uma ação sobe a outra cai ou sobe menos e quando uma cai a outra sobe ou cai menos, de forma a diminuir a variação absoluta do retorno da carteira.
Com base em uma expectativa de retorno formada de alguma maneira (não analisada neste artigo), deve-se escolher os ativos para compor a carteira e seus respectivos pesos, levando em conta a variabilidade esperada dos retornos (o desvio-padrão dos retornos). Essa variabilidade dos retornos em torno da média é uma medida do risco de uma ação e o risco de uma carteira pode ser reduzido através da diversificação. O que se deseja na composição de uma carteira é maximizar o retorno esperado dado um nível de risco.
loading...
- Com Quantas Ações Se Faz Uma Carteira Bem Diversificada?
Desde o trabalho seminal de Harry Markowitz que o potencial de redução de risco proporcionado pela diversificação está bem estabelecido. Uma questão mais prática é: precisamos de quantas ações para obter uma carteira “bem diversificada”....
- Estilos De Investimentos
Em artigopublicado no Journal of Portfolio Management em 1978, William Sharpe explica sobre os estilos de investimentos de uma maneira interessante e bastante técnica. Basicamente, são quatro estilos de investimentos listados por Sharpe, gestão passiva...
- Avaliação De Desempenho De Carteiras
Os modelos do texto anterior podem ser modificados para se tornarem medidas de desempenho de carteiras. Podem ainda ser utilizados para analisar retornos de ativos individuais (carteiras de um ativo), sendo que isso não é comum para os dois primeiros....
- βeta
No cálculo de retornos exigidos de ações para avaliação de empresas (taxa de desconto), gestão de investimentos (retorno esperado) ou finanças corporativas (custo do capital próprio), usa-se comumente a seguinte fórmula: Retorno Exigido: Taxa...
- Risco E Retorno (renda Variável)
Risco e Retorno são dois conceitos essenciais em Finanças, conceitos intimamente ligados. Esse post tratará especificamente do risco e do retorno para ativos de renda variável, não tratando da renda fixa. O retorno passado de um ativo é a sua valorização...
